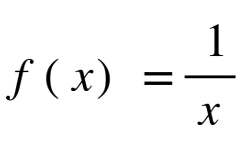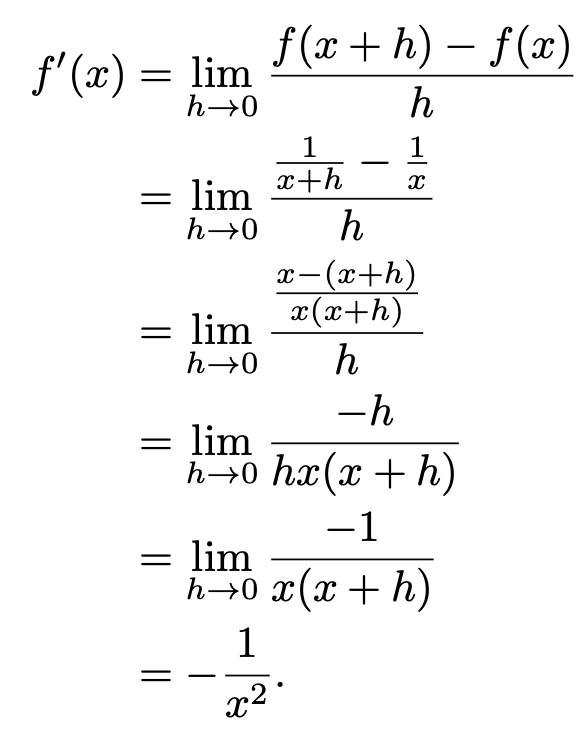The gradient at any point on a curve is defined as the gradient of the tangent at that point to the curve. Consider a curve y = f(x) with a fixed point A(x, f(x)). How do we find the gradient of the curve at A?
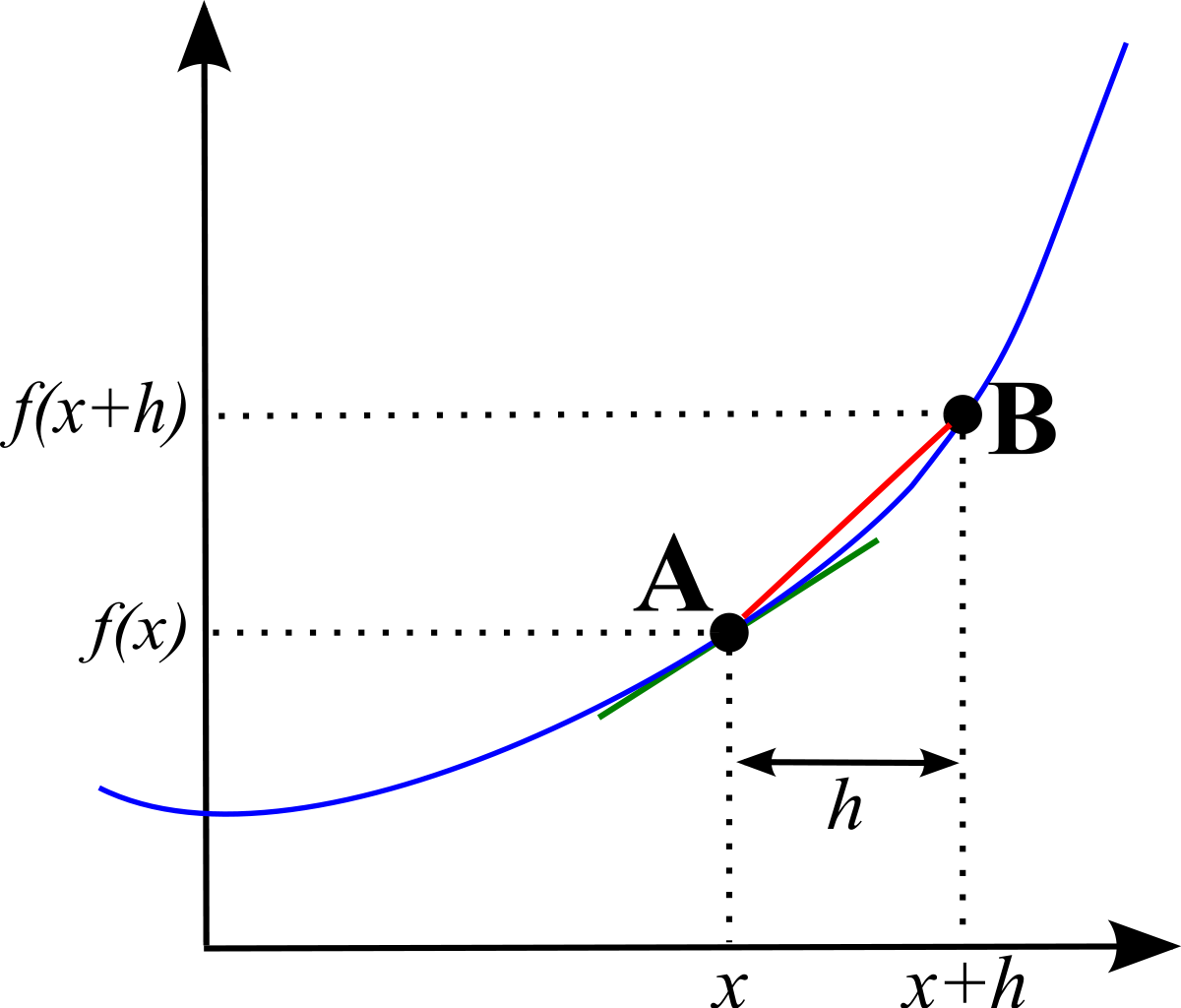
First, we consider another point on the curve, B(x+h, f(x+h)). Drawing a chord between points A and B, we know that:
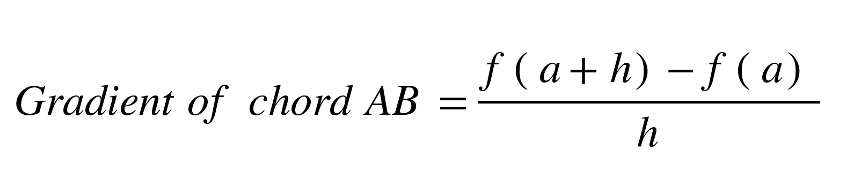
As h gets smaller and smaller, the gradient of this chord approaches the gradient of the line tangent to the graph at A.
Hence, we can define the gradient at a point to be:
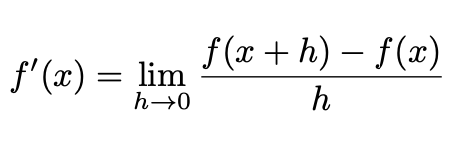
This process of using the limit as h approaches 0 to find the gradient is known as differentiation by first principles.
Example: